| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 몽상 드 애월
- 리뷰
- 올레식당
- 지디카페
- 파이썬
- 단어장
- 책
- 여행
- 맛집
- 서평
- 제주
- 개발
- 여행코스
- 혼밥
- 설치
- 여자혼자
- 제주도
- 영어 단어
- OpenGL
- 그림으로 원서 읽기
- 영어
- CG
- 그래픽스
- 관광
- 관광코스
- python
- 원서
- James and the Giant Peach
- 그래픽스 요약 정리
- 독후감
- Today
- Total
JUST DO IT PROJECT
Efficient Geometrically Exact Continuous Collision Detection (SIGGRAPH 2012) 본문
Efficient Geometrically Exact Continuous Collision Detection (SIGGRAPH 2012)
웨일.K 2020. 3. 5. 03:50What is CCD?
이 논문을 이해하기 위해서는 먼저 Continuous Collision Detection (이하 CCD)가 무엇인지 알 필요가 있습니다.
(http://www.stencyl.com/help/view/continuous-collision-detection/)
애니메이션, 시뮬레이션에서 사용되는 물리 엔진에서는 한 타임스텝마다 물체간의 충돌 검사를 합니다. 만약 어떤 시점에 두 물체가 충돌하면 아래와 같이 밀어내버립니다. 이때 물체간의 충돌이 있는지 여부를 알아내는 것을 충돌 감지(Collision Detection)이라고 하고, 두 물체가 겹치지 않게 떼어내주는 것을 충돌처리(Collision Response)라고 합니다.

그런데 물체가 너무 빨리 지나가면 아래 그림과 같이 종종 물체의 겹침을 포착하지 못하고 충돌 감지에 실패하는 경우가 생깁니다. 이를 Tunnelling이라고 합니다.
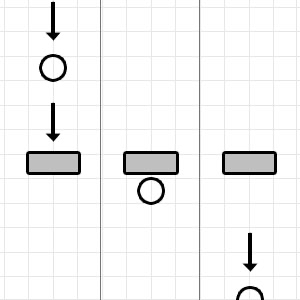
이 문제를 해결하기 위해서 나온 것이 CCD입니다. 한 타임스텝동안 물체가 움직일 때, 시작점의 위치와 끝 지점의 위치 사이에 있는 모든 포지션에서 (그림의 자주색 라인) 그 사이에 다른 물체가 있는지 체크하는 것이죠. 물체가 있으며 해당 타임스텝에 충돌이 있었다고 봅니다.

이 논문에서는 이 CCD 를 효과적으로, 정확하게 하는 방법에 대해 논합니다. 기하학적인 접근방식을 사용해서요.
논문 목차
Efficient Geometrically Exact Continuous Collision Detection
Abstract
1. INTRO
2. RELATED WORK
a. Cubic Solver
b. Other works in CCD
c. Exact Geometric Computation
3. CCD in 3D
a. Root Parity
b. Ray-Bilinear-Patch Crossing Parity Testing
c. Together
4. Implementation
a. Resolving Collision
5. Examples
6. ConclusionsABSTRACT
기존에는 3차 방정식을 풀어서 해결했지만, 이는
- Rounding error(반올림에서 기인하는 오차)에 취약하고
- Ad hoc tolerances가 필요하고, 면에 대해서는 취약한 단점이 있고,
- 또 시뮬레이션마다 튜닝을 하는데도 불구하고, 충돌이 누락되거나 (false negatives), 충돌이 아닌데도 충돌이라고 감지하는 경우(false positives)가 종종 있었음.
따라서 이 논문에서 제안하는 방법은
- Geometrically Exact 방식, 결과가 Boolean으로 제공.
- 발견한 인사이트: robust 시뮬레이션을 위해서는 몇 번 충돌했는지 그 parity만 필요함. (짝/홀)
- 이 Parity는 간단한 non-constructive Predicates로 계산할 수 있음.
Parameter domain의 경계를 고려해서 CCD를 정의하고 그 방정식의 해를 분석함. - Conservative culling, interval filters를 사용해서 tuning 없이도 빠르게 잘 돌아가게 함.
- 이걸 이용해서 Cloth 시뮬레이션을 구현했는데. Remashing이 자주 일어나는데도 intersection-free한 상태를 유지함.
1. Introduction
- CCD: mesh가 움직일 때, 시작과 끝 지점 사이에 자기자신과 충돌하는 점이 있는지 체크하는 것으로 정의
- Safe : no false negatives (충돌 누락 x)
- Accurate: false positives 최소화 (충돌 아닌데 충돌이라고 하는 거)
1) CCD 알고리즘
: safety, accuracy 만족하고 Boolean answer 제공
2) Ray- blilinear patch intersection parity test
: 점이 쿼드메시 안에 존재하는지 체크
3) Cloth simulation
: remeshing이 일어나는데도 intersection-free한 상태 유지. 성능에 하자 없음을 보여줌.
2. Related Work
1) Cubic Solver
- 삼차방정식 풀어서 시간구하고 그 시간에 충돌이 진짜 일어났는지
- 허용오차를 둬서 false negatives (충돌 누락) 줄임 (작은 거리 안에 두 메시 있으면 충돌)
- 근데 허용오차를 얼마로 해야 하는지 사전에 예측하기가 어려움.
- 삼차방정식 풀면 해가 irrational 하기도 하고, 중간중간 rounding error 트래킹 어려움
- 시뮬레이션마다 적절한 시행착오 겪으면서 허용오차를 찾아야 함
- General purpose library를 만들기 어려움
- 허용오차 크면 False positive (충돌 아닌데 충돌이라고) 발생해서 느려짐
- fully symbolic implementation을 쓰면 해결할 수 있지만 계산량 많아.
==> 논문에서 제시하는 방식을 쓰면 이런 허용오차 튜닝 없이 safe 하고 accurate 한 CCD를 할 수 있다.
2) Other Work in CCD
- 여러가지 CCD 방법들이 있으나 대부분
i. User-set tolerance에 의존하거나
ii. Rounding error문제가 있음 - Raytracing 같은 경우는 이 논문에서 차용해서
i. Ray vs bilinear patch intersection parity test에 사용했음
ii. 위치를 찾는 기존 방법들과 다르게 교점의 parity 만 제공하기 때문에 rounding error에서 벗어남 - Culling collision test도 연구가 많이 되었는데
이 논문의 포커스는 culling method의 효율성보다는 core element 끼리의 테스트에서의 정확성에 있음
3) Exact Geometric Computation
- 삼차방정식 푸는건 constructive geometric algorithm인데, 중간 값들을 계산에 연속적으로 사용하기 때문에 중간중간 발생하는 rounding error를 트래킹하기 어렵다.
- 대안: 몇 개의 Predicate set을 만들어서 discrete answer를 내도록 하는 방법
i. ex. 점이 선 왼쪽에 있나? 오른쪽에 있니? 선 위에 있나?
ii. 그럼 predicate을 정의하는 것이 중요함. 여러가지 방법들이 있고 제일 성공적인게 EGC - 이 논문에서는 intersection test set으로 나눠서 CCD 진행하고
- Fast interval arithmetic filter도 사용함.
3. CCD in 3D
- Point-triangle / Segment-segment 두가지 충돌 테스트가 있음
- Input이 8개의 점.(시작4개 끝 4개)
- 시간에 따른 Vector 함수를 다음과 같이 정의할 수 있음.
- P-T 경우: 움직이는 점 0, 삼각형 1,2,3 도메인은 삼각프리즘
- S-S 경우: 선분 0,1 선분 2,3 으로 도메인은 유닛큐브
- 충돌 감지:
○ 도메인 경계상에 원점이 있거나
○ 도메인 내에 해가 홀수개인 경우
○ 짝수개일 때는 무시. 충돌일 수 없음.
1) Determining Root Parity
a. 도메인을 가지고 F 경계를 만듦.
i. 1-1 인경우는 원점이 F에 포함되는지 그림 2에서 해가 없기 때문에 원점이 포함안됨
ii. 1-1 아니면 해의 개수 parity가 odd
b. 알고리즘:: 다음의 경우는 충돌이다.
i. F 경계가 원점을 포함한다
ii. 원점에서 임의의 방향으로 레이를 쏘았을 때 F와의 교점이 홀수개다.
(경계랑 평행하거나 하면 다시 쏜다)
c. 도메인을 육면체나 프리즘으로 만들어서 ray casting을 하는데
i. 육면체나 프리즘 모두 bilinear patches를 가질수 있음
ii. 레이-삼각형은 가능한데 레이-BP는 없음.
==> 본 논문에서 효율적으로 parity 계산하는 법을 제시2) Ray vs Bilinear-Patch Crossing Parity Testing
- 한쪽은 + 한쪽은 -인 scalar function
- bilinear patch의 네 점을 꼭지점으로 하는 사면체에서
- 두 삼각형을 짝으로 지어서 한 pair는 + 나머지 한 pair는 -
- Ray 원점이 사면체 안에 있나 없나 체크
○ 안에 있으면: 이제 ray- patch 테스트는 두개의 ray-triangle 테스트가 됨
§ 원점의 부호와 반대인 삼각형- 레이사이에 교점이 있으면 patch와도 교점이 있음
○ 밖에 있으면: 사면체를 patch의 proxy로 이용가능. 그래서 레이와 사면체의 교점 개수는 patch와의 개수랑 같음3) Put Together
Parity 계산은
- 선분-선분이면 도메인 육면체니까 6개 ray patch
- 점-삼각형이면 도메인 프리즘이니까 3개 ray patch, 2개 ray triangle
- 각 계산의 교점 개수 합계가 홀수개면 충돌.
- 특별케이스
○ 원점이 패치나 삼각형 위에 있으면 ? 충돌 / 레이 캐스팅 안함
○ Ray가 두 패치/삼각형이 접한 선분 위의 점에 닿으면? 레이 다른 방향으로 쏴요4. Implementation
: 빠르고 효율적인 방법으로 구현해야 하므로 필터와 culling을 사용했음
- 필터
- Culling (AABB) 사용해서 겹치는 부분에서만 충돌감지를 실행Resolving Collision
- 여기까지는 충돌 감지였는데, 그럼 충돌을 어떻게 피하냐?
- 이상적인 물리적 해결방법으로는 너무 큰 정수계산이 필요
여기서는 속도 필터링 접근
i. 먼저 대강의 mesh에 반발력 적용시킨 후,
ii. CCD를 진행하고
iii. 충돌이 일어나면 각각에다 적용 - 이전의 연구들은 충돌지점의 normal을 사용했지만
- 이 논문에서는 t=0.5일 때 가장 가까운 점사이의 벡터로 노말을 구해도 괜찮았음.
- 그게 더 계산할 때 효율적
5. Example
- 처음부터 커브 져 있는 천 40x400 vertex를 바닥에 떨어뜨리는 예제
- Self-collision 많이 일어남
- Remeshing 의 장점은
○ 에러 줄이고, 작은 부분에서 계산을 집중할 수 있다는 것
○ 천의 경우는 굴곡진 부분에서 density 를 증가시킬 수 있다는 것 - 몇몇 사람들이 시뮬레이션 개선하려고 했지만 충돌처리 때문에 힘들었다.
- 이 논문의 parametrless collision detection system으로 FEM시뮬레이터를 만들 수 있었다.
○ 돌아가는 공 위에 천 떨어뜨리거나, 여러겹의 천 떨어뜨리는 시뮬레이션도 잘 돌아감. - CCD 부르는데 쓰는 평균 시간은 AABB culling 제외하고 seg-seg는 614, point-trisms 439. 기존 삼차함수 푸는것보다 빠름.
- Call 당 평균 시간은 culling 없이는 기존보다 느림, culling이 아주 효과가 좋음을 알 수 있음.
6. Conclusion
의의: 충돌감지문제
- 주어진 도메인에서 홀수개의 해를 가지는 함수인지 결정하는 문제
- 레이와 도메인 경계 간 교점 parity 문제로
- ray-triangle, ray-patch 문제로 감소시켰다는 것.
구현 단계:
- Floating point filter, interval arithmetic을 써서 효율을 높였고
- 까다로운 예제로 유용성도 증명했다는 것.
CCD를 명시적으로 다룬 천 시뮬레이션으로는 처음.
이런 방식이 다른 분야에도 적용될 수 있다.
'Research > Paper Reviews' 카테고리의 다른 글
| As-Rigid-As-Possible Surface Modeling (2007) (0) | 2018.05.31 |
|---|
